勾股定理的历史 勾股定理在中国以及外国的历史_勾股数的定义 勾股定理最简单的方法
勾股定理的历史 勾股定理在中国以及外国的历史
1、中国:公元前十一世纪,周朝数学家商高就提出“勾三、股四、弦五”。《周髀算经》中记录着商高同周公的一段对话。商高说:“…故折矩,勾广三,股修四,经隅五。”意为:当直角三角形的两条直角边分别为3(勾)和4(股)时,径隅(弦)则为5。以后人们就简单地把这个事实说成“勾三股四弦五”,根据该典故称勾股定理为商高定理。
2、公元三世纪,三国时代的赵爽对《周髀算经》内的勾股定理作出了详细注释,记录于《九章算术》中“勾股各自乘,并而开方除之,即弦”,赵爽创制了一幅“勾股圆方图”,用形数结合得到方法,给出了勾股定理的详细证明。后刘徽在刘徽注中亦证明了勾股定理。在中国清朝末年,数学家华蘅芳提出了二十多种对于勾股定理证法。
3、外国:远在公元前约三千年的古巴比伦人就知道和应用勾股定理,他们还知道许多勾股数组。美国哥伦比亚大学图书馆内收藏着一块编号为“普林顿322”的古巴比伦泥板,上面就记载了很多勾股数。古埃及人在建筑宏伟的金字塔和测量尼罗河泛滥后的土地时,也应用过勾股定理。
4、公元前六世纪,希腊数学家毕达哥拉斯证明了勾股定理,因而西方人都习惯地称这个定理为毕达哥拉斯定理。
5、公元前4世纪,希腊数学家欧几里得在《几何原本》(第ⅰ卷,命题47)中给出一个证明。
6、1876年4月1日,加菲尔德在《新英格兰教育日志》上发表了他对勾股定理的一个证法。
7、1940年《毕达哥拉斯命题》出版,收集了367种不同的证法。
勾股数的定义 勾股定理最简单的方法
勾股数的定义是什么
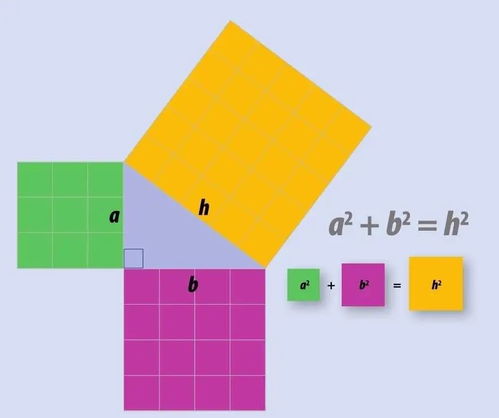
勾股定理又称勾股弦定理、勾股定理,是一个基本的几何定理,指直角三角形的两条直角边长(古称勾长、股长)的平方和等于斜边长(古称弦长)的平方。它是数学定理中证明方法最多的定理之一,也是数形结合的纽带之一。中国古代称直角三角形为勾股形,并且直角边中较小者为勾,另一长直角边为股,斜边为弦,故称之为勾股定理。
勾3股4弦5是著名的勾股定理。当直角三角形的两条直角边分别为3(短边)和4(长边)时,径隅(就是弦)则为5。以后人们就简单地把这个事实说成“勾三股四弦五”
勾股数是什么
定义:三个数满足两个的平方和等于第三个数的平方也就是满足勾股定理,就称这三个数是勾股数。
解释:1楼说的对,3”+4”=5”(3,4,5就是勾股数)注明(”表示平方)
勾股数是什么意思?
勾股数又名毕氏三元数
凡是可以构成一个直角三角形三边的一组正整数,称之为勾股数。
①观察3,4,5;5,12,13;7,24,25;…发现这些勾股数都是奇数,且从3起就没有间断过。计算0.5(9-1),0.5(9+1)与0.5(25-1),0.5(25+1),并根据你发现的规律写出分别能表示7,24,25的股和弦的算式。
勾股数的定义 勾股定理最简单的方法
②根据①的规律,用n的代数式来表示所有这些勾股数的勾、股、弦,合情猜想他们之间的两种相等关系,并对其中一种猜想加以说明。
③继续观察4,3,5;6,8,10;8,15,17;…可以发现各组的第一个数都是偶数,且从4起也没有间断过,运用上述类似的探索方法,之间用m的代数式来表示它们的股合弦。
设直角三角形三边长为a、b、c,由勾股定理知a^2+b^2=c^2,这是构成直角三角形三边的充分且必要的条件。因此,要求一组勾股数就是要解不定方程x^2+y^2=z^2,求出正整数解。
例:已知在△ABC中,三边长分别是a、b、c,a=n2-1,b=2n,c=n2+1(n>1),求证:∠C=90°。此例说明了对于大于2的任意偶数2n(n>1),都可构成一组勾股数,三边分别是:2n、n2-1、n2+1。如:6、8、10,8、15、17,10、24、26…等。
再来看下面这些勾股数:3、4、5,5、12、13,7、24、25,9、40、41,11、60、61…这些勾股数都是以奇数为一边构成的直角三角形。由上例已知任意一个大于2的偶数可以构成一组勾股数,实际上以任意一个大于1的奇数2n+1(n>1)为边也可以构成勾股数,其三边分别是2n+1、2n2+2n、2n2+2n+1,这可以通过勾股定理的逆定理获证。
观察分析上述的勾股数,可看出它们具有下列二个特点:
1、直角三角形短直角边为奇数,另一条直角边与斜边是两个连续自然数。
2、一个直角三角形的周长等于短直角边的平方与短边自身的和。
掌握上述二个特点,为解一类题提供了方便。
例:直角三角形的三条边的长度是正整数,其中一条短直角边的长度是13,求这个直角三角形的周长是多少?
用特点1解:设这个直角三角形三边分别为13、x、x+1,则有:169+x2=(x+1)2,解得x=84,此三角形周长=13+84+85=182。
用特点2解:此直角三角形是以奇数为边构成的直角三角形,因此周长=169+13=182。
勾股数的通项公式:
题目:已知a^2+b^2=c^2,a,b,c均为正整数,求a,b,c满足的条件.
解答:
结论1:从题目中可以看出,a+b>c (1),联想到三角形的成立条件容易得出。
结论2:a^2=c^2-b^2=(c+b)*(c-b) (2)
从(2)中可以看出题目的关键是找出a^2做因式分解的性质,令X=c+b,Y=c-b
所以:a^2=X*Y,(X>Y,a>Y) (3)
首先将Y做分解,设Y的所有因子中能写成平方数的最大的一个为k=m^2,所以Y=n*m^2 (4)
又(3)式可知a^2=X*n*m^2 (5)
比较(5)式两边可以a必能被m整除,且n中不可能存在素数的平方因子,否则与(4)中的最大平方数矛盾。
勾股数的定义 勾股定理最简单的方法
同理可知a^2=Y*n'*m'^2 (6),X=n'*m'^2,且 n'为不相同素数的乘积
将(5)式与(6)式相乘得a^2=(m*m')^2*n'*n,(n,n'为不相同素数的乘积) (7)
根据(7)知n*n'仍然为平方数,又由于n',n均为不相同素数乘积知n=n'(自行证明,比较简单)
可知a=m'*m*n
c=(X+Y)/2=(n*m^2+n*m'^2)/2=n*(m^2+m'^2)/2
b=(X-Y)/2=n*(m'^2-m^2)/2
勾股数的定义 勾股定理最简单的方法
a=m*n*m'
[编辑本段]勾股数的常用套路
所谓勾股数,一般是指能够构成直角三角形三条边的三个正整数(a,b,c)。
即a^2+b^2=c^2,a,b,c∈N
又由于,任何一个勾股数组(a,b,c)内的三个数同时乘以一个整数n得到的新数组(na,nb,nc)仍然是勾股数,所以一般我们想找的是a,b,c互质的勾股数组。
关于这样的数组,比较常用也比较实用的套路有以下两种:
1、当a为大于1的奇数2n+1时,b=2*n^2+2*n, c=2*n^2+2*n+1。
实际上就是把a的平方数拆成两个连续自然数,例如:
n=1时(a,b,c)=(3,4,5)
n=2时(a,b,c)=(5,12,13)
n=3时(a,b,c)=(7,24,25)
... ...
这是最经典的一个套路,而且由于两个连续自然数必然互质,所以用这个套路得到的勾股数组全部都是互质的。
2、当a为大于4的偶数2n时,b=n^2-1, c=n^2+1
也就是把a的一半的平方分别减1和加1,例如:
n=3时(a,b,c)=(6,8,10)
n=4时(a,b,c)=(8,15,17)
n=5时(a,b,c)=(10,24,26)
n=6时(a,b,c)=(12,35,37)
... ...
这是次经典的套路,当n为奇数时由于(a,b,c)是三个偶数,所以该勾股数组必然不是互质的;而n为偶数时由于b、c是两个连续奇数必然互质,所以该勾股数组互质。
所以如果你只想得到互质的数组,这条可以改成,对于a=4n (n>=2), b=4*n^2-1, c=4*n^2+1,例如:
n=2时(a,b,c)=(8,15,17)
n=3时(a,b,c)=(12,35,37)
n=4时(a,b,c)=(16,63,65)
... ...
========Edward补充========
对于N 为质因数比较多的和数时海可以参照其质因数进行 取相应的勾股数补充,即1个N会有多对的勾股数,例如:
n=9时(a,b,c)=(9,24,25)or (9,12,15) --------3* (3,4,5)
n=12时(a,b,c)= (12,35,37) or (12,16,20) ----- 4*(3,4,5)
=========ShangJingbo补充=======
还有诸如此类的勾股数,20、21、29;
119、120、169;
696、697、985;
4059、4060、5741;
23660、23661、33461;
137903 137904 195025
803760 803761 1136689
4684659 4684660 6625109
……
已有三千年研究历史的勾股定理还有研究的空间吗? 我用本文试探索。
勾 股 数
1. 定义:凡符合X^2+Y^2=Z^2公式的正整数值我们称之为勾股数。X和Y是直角边,Z是斜边。
2. 凡有公约数的勾股数我们称之为派生勾股数,例[30,40,50] 等;
3. 无公约数的勾股数,例[3,4,5];[8,15,17]等,我们称之为勾股数。全是偶数的勾股数必是派生勾股数,三个奇数不可能符合定义公式。因此,勾股数唯一的可能性是:
X和Y分别是奇数和偶数(偶数和奇数),斜边Z只能是奇数。
4. 勾股数具有以下特性:
斜边与偶数边之差是奇数,这个奇数只能是某奇数的平方数, 例1,9,25,49,……,至无穷大;
斜边与奇数边之差是偶数,这个偶数只能是某偶数平方数的一半, 例2,8,18,32,……,至无穷大;
5. 由以上定义我们推导出勾股公式:
X = P^2 + PQ (X等于P平方加PQ)
Y = Q^2/ 2 + PQ (Y等于二分之Q方加PQ)
Z = P^2 + Q^2 / 2 + PQ (Z等于P平方加二分之Q方加PQ)
6. 此公式涵盖了自然界的全部勾股数,包括派生勾股数。
7. 用此公式很容易导出全部勾股数,例如2000以内的勾股数计有320组,(不含派生勾股数)。最大的一组是 [315, 1972, 1997]
8. 斜边是1105和1885的勾股数各有4组:
[47,1104,1105] [264,1703,1105] [576,943,1105] [744,817,1105];
[427,1836,1885] [1003,1596,1885] [1643,924,1885] [1813,516,1885];
9. 以任意奇数代入P ,任意偶数代入Q ,即可得到唯一一组勾股数。
例如P = 5 ,Q = 8 ,得到
X = 25 + 5×8 = 65
Y = 32 + 5×8 = 72
Z = 25 + 32 + 5×8 = 97
10. 它极清楚地显示出了斜边与偶数直角边之差是奇数的平方,斜边与奇数直角边之差是偶数平方值的一半,而斜边则是由奇数的平方与偶数平方的一半和此奇数与偶数之积三项之和所构成。
11. 当P与Q有公约数时,例如9与12 ,再例如21与28等,推导出来的是派生勾股数;
当P与Q无公约数时,例如9 与8 ,再例如21与16等,推导出来的是勾股数;
12. 不存在不符合本公式的勾股数。例如有人奉献趣味勾股数[88209,90288,126225],它实际 是个派生勾股数,它是[297,304,425]乘297倍而成,它是由P = 11和Q = 16导出。
13. 本文所提供的公式是依据本文第4条的两条勾股数特性规律推导而出,但是它可以与六百年前印度婆罗门笈多公式相互推导。
14. 依据本公式勾股定理可从正整数拓展到负整数。在笛卡尔座标图上,勾股三角形可以在更大的位置上显现。
[编辑本段]勾股数公式及证明
a=2mn
b=m^2-n^2
c=m^2+n^2
证:
假设a^2+b^2=c^2,这里研究(a,b)=1的情况(如果不等于1则(a,b)|c,两边除以(a,b)即可)
如果a,b均奇数,则a^2 + b^2 = 2(mod 4)(奇数mod4余1),而2不是模4的二次剩余,矛盾,所以必定存在一个偶数。不妨设a=2k
等式化为4k^2 = (c+b)(c-b)
显然b,c同奇偶(否则右边等于奇数矛盾)
作代换:M=(c+b)/2, N=(c-b)/2,显然M,N为正整数
现在往证:(M,N)=1
如果存在质数p,使得p|M,p|N, 那么p|M+N(=c), p|M-N(=b), 从而p|c, p|b, 从而p|a,这与(a,b)=1矛盾
所以(M,N)=1得证。
依照算术基本定理,k^2 = p1^a1 * p2^a2 * p3^a3 * ...,其中a1,a2...均为偶数,p1,p2,p3...均为质数
如果对于某个pi,M的pi因子个数为奇数个,那N对应的pi因子必为奇数个(否则加起来不为偶数),从而pi|M, pi|N,(M,N)=pi>1与刚才的证明矛盾
所以对于所有质因子,pi^2|M, pi^2|N,即M,N都是平方数。
设M = m^2, N = n^2
从而有c+b = 2m^2, c-b = 2n^2,解得
勾股定理在生活中的应用
勾股定理:在平面上的一个直角三角形中,两个直角边边长的平方和等于斜边长的平方。
勾股定理在生活中的应用:
装修问题。工人为了判断一个墙角是否为标准直角,可利用勾股定理进行判断;
地毯费用问题。在已知高和斜坡长的楼梯表面铺地毯,可利用勾股定理计算地毯的长度。
100以内勾股数表 勾股定理最简单的方法
求100以内的勾股数(整数)
3 4 56 8 109 12 1512 16 2015 20 2518 24 3021 28 3524 32 4027 36 4530 40 5033 44 5536 48 6039 52 6542 56 7045 60 7548 64 8051 68 8554 72 9057 76 9560 80 100 此为一类5 12 1310 24 2615 36 3920 48 5...
前100组勾股数
楼主啊看看,我说得对不.
100以内的勾股数有16组:
3,4,5;
5,12,13;
8,15,17;
7,24,25;
21,22,29;
12,35,37;
9,40,41;
28,45,53;
11,60,61;
33,56,65;
16,63,65;
48,55,73;
13,84,85;
100以内勾股数表 勾股定理最简单的方法
36,77,85;
39,80,89;
65,72,97;
绝对对的,我可是花了一点时间算出来的哦.
写出100 组勾股数组
楼主啊看看,我说得对不.
100以内的勾股数有16组:
3,4,5;
5,12,13;
8,15,17;
7,24,25;
21,22,29;
12,35,37;
9,40,41;
28,45,53;
11,60,61;
33,56,65;
16,63,65;
48,55,73;
13,84,85;
36,77,85;
39,80,89;
65,72,97;
绝对对的,我可是花了一点时间算出来的哦.
100以内勾股数表及顺口溜
100以内勾股数表及顺口溜具体如下:
3,4,5:勾三股四弦五。
5,12,13:5月12记一生(13)。
6,8,10:连续的偶数。
8,15,17:八月十五在一起(17)。
特殊勾股数:
连续的勾股数只有3,4,5。
连续的偶数勾股数只有6,8,10。
勾股表如下:
a
b
c
3
4
5
5
12
13
6
8
10
7
24
25
8
15
17
9
12
15
9
40
41
10
24
26
11
60
61
12
16
20
12
35
37
13
84
85
14
48
50
15
20
25
15
36
39
16
30
34
16
63
65
18
24
30
18
100以内勾股数表 勾股定理最简单的方法
80
82
20
21
29
20
48
52
21
28
35
21
72
75
24
32
40
24
45
51
24
70
74
25
60
65
27
36
45
28
45
53
28
96
100
30
40
50
30
72
78
32
60
68
33
44
55
33
56
65
35
84
91
36
48
60
36
77
85
39
52
65
39
80
89
40
42
58
40
75
85
42
56
70
45
60
75
48
55
75
48
64
80
51
68
85
57
76
95
60
63
87
60
80
100以内勾股数表 勾股定理最简单的方法
100
65
72
97
100以内的常见勾股数有哪些?
勾股数的一般解为x=l(m^2-n^2),y=l(2mn),z=l(m^2+n^2),m和n为一奇一偶,l为任意正整数。
因为z<=100,所以l(m^2+n^2)<=100,接下来就可以一个个写出来了,如m=2,n=1,l=1时,x=3,y=4,z=5
m=3,n=2,l=4时,x=5*4=20,y=12*4=48,z=13*4=52
……
等等,楼主自己继续吧。
勾股定理证明图(勾股定理10种证明方法附图)
小周今天给分享勾股定理证明图的知识,其中也会对勾股定理10种证明方法附图进行解释,希望能解决你的问题,请看下面的文章阅读吧!
勾股定理证明图(勾股定理10种证明方法附图)
1、证法1:(梅文鼎证明) 做四个全等的直角三角形,设它们的两条直角边长分别为a、b ,斜边长为c. 把它们拼成如图那样的一个多边形,使D、E、F在一条直线上. 过C作AC的延长线交DF于点P。
2、 ∵ D、E、F在一条直线上, 且RtΔGEF ≌ RtΔEBD, ∴ ∠EGF = ∠BED, ∵ ∠EGF + ∠GEF = 90°, ∴ ∠BED + ∠GEF = 90°, ∴ ∠BEG =180°―90°= 90° 又∵ AB = BE = EG = GA = c, ∴ ABEG是一个边长为c的正方形. ∴ ∠ABC + ∠CBE = 90° ∵ RtΔABC ≌ RtΔEBD, ∴ ∠ABC = ∠EBD. ∴ ∠EBD + ∠CBE = 90° 即 ∠CBD= 90° 又∵ ∠BDE = 90°,∠BCP = 90°, BC = BD = a. ∴ BDPC是一个边长为a的正方形. 同理,HPFG是一个边长为b的正方形. 设多边形GHCBE的面积为S,则 ∴ ,即 a^2+b^2=S+2*1/2ab c^2=S+2*1/2ab ∴ a^2+b^2=c^2 证法2:(项明达证明) 做两个全等的直角三角形,设它们的两条直角边长分别为a、b(b>a) ,斜边长为c. 再做一个边长为c的正方形. 把它们拼成如图所示的多边形,使E、A、C三点在一条直线上. 过点Q作QP∥BC,交AC于点P. 过点B作BM⊥PQ,垂足为M;再过点 F作FN⊥PQ,垂足为N. ∵ ∠BCA = 90°,QP∥BC, ∴ ∠MPC = 90°, ∵ BM⊥PQ, ∴ ∠BMP = 90°, ∴ BCPM是一个矩形,即∠MBC = 90°. ∵ ∠QBM + ∠MBA = ∠QBA = °, ∠ABC + ∠MBA = ∠MBC = 90°, ∴ ∠QBM = ∠ABC, 又∵ ∠BMP = 90°,∠BCA = 90°,BQ = BA = c, ∴ RtΔBMQ ≌ RtΔBCA. 同理可证RtΔQNF ≌ RtΔAEF. 证法3:(欧几里得证明) 做三个边长分别为a、b、c的正方形,把它们拼成如图所示形状,使H、C、B三点在一条直线上,连结BF、CD. 过C作CL⊥DE,交AB于点M,交DE于点L。
3、 ∵ AF = AC,AB = AD,∠FAB = ∠GAD, ∴ ΔFAB ≌ ΔGAD, ∵ ΔFAB的面积等于, ΔGAD的面积等于矩形ADLM的面积的一半, ∴ 矩形ADLM的面积 =矩形MLEB的面积 ∵ 正方形ADEB的面积= 矩形ADLM的面积 + 矩形MLEB的面积 ∴ ,即 a^2+b^2=c^2 扩展资料 勾股定理是一个基本的几何定理,指直角三角形的两条直角边的平方和等于斜边的平方。
4、 中国古代称直角三角形为勾股形,并且直角边中较小者为勾,另一长直角边为股,斜边为弦,所以称这个定理为勾股定理,也有人称商高定理。
5、 勾股定理现约有500种证明方法,是数学定理中证明方法最多的定理之一。
6、 勾股定理是人类早期发现并证明的重要数学定理之一,用代数思想解决几何问题的最重要的工具之一,也是数形结合的纽带之一。
7、 在西方,最早提出并证明此定理的为公元前6世纪古希腊的毕达哥拉斯学派,他用演绎法证明了直角三角形斜边平方等于两直角边平方之和。
本文到这结束,希望上面文章对大家有所帮助。
勾股定理什么年级学的
初二上学期第一单元开始学习勾股定理。勾股定理又称商高定理、毕达哥拉斯定理,简称“毕氏定理”,是平面几何中一个基本而重要的定理。勾股定理说明,平面上的直角三角形的两条直角边的长度(古称勾长、股长)的平方和等于斜边长(古称弦长)的平方。
勾股定理简介
1、勾股定理的证明是论证几何的发端。
2、勾股定理是历史上第一个把数与形联系起来的定理,即它是第一个把几何与代数联系起来的定理。
3、勾股定理导致了无理数的发现,引起第一次数学危机,大大加深了人们对数的理解。
4、勾股定理是历史上第—个给出了完全解答的不定方程,它引出了费马大定理。
5、勾股定理是欧氏几何的基础定理,并有巨大的实用价值。这条定理不仅在几何学中是一颗光彩夺目的明珠,被誉为“几何学的基石”,而且在高等数学和其他科学领域也有着广泛的应用。
勾股定理是几年级学的 你知道吗
初二上学期第一单元开始学习勾股定理。八年级下册,第十九章《勾股定理》(沪科版)也就是八下的第三章,期中考试一般就考到这里。p 股定理p 股定理逆定理p小结。
勾股定理是一个基本的几何定理,指直角三角形的两条直角边的平方和等于斜边的平方。
勾股定理,直角三角形的两条直角边的平方和等于斜边的平方.
abc/p>
c=√(ab
√(=√√/p>
勾股定理是几年级学的 你知道吗
1、初二上学期第一单元开始学习勾股定理。八年级下册,第十九章《勾股定理》(沪科版)也就是八下的第三章,期中考试一般就考到这里。p50. 19.1勾股定理p58. 19.2勾股定理逆定理p64.小结。
2、勾股定理是一个基本的几何定理,指直角三角形的两条直角边的平方和等于斜边的平方。
3、勾股定理,直角三角形的两条直角边的平方和等于斜边的平方.
4、a2+b2=c2
5、c=√(a2+b2)
6、√(1202+902)=√22500=√1502=150
初二数学下册单元考试《勾股定理》
这篇关于初二数学下册单元考试《勾股定理》,是








