下面的code完美的作品，但我想有人向我解释数学后面。基本上，它是如何工作的？

 的#include＆LT; stdio.h中＆GT;
＃包括＆LT; stdlib.h中＆GT; / *的atoi * /

的#define分钟（X，Y）（（（x）的≤（Y））（X）：（y））为

INT主（INT ARGC，字符* argv的[]）
{
   const int的基础= 16;
   INT N，I，J，P，C，NOZ，K;

   N = 7; / * 7！ =十进制5040或0x13B0  -  1尾随零* /
   NOZ = N;
   J =基地;
   / *为什么我们从2开始* /
   对于（i = 2; I＆LT; =基地;我++）
   {
      如果（j％我== 0）
      {
         p值= 0; / *什么是对？ * /
         而（j％我== 0）
         {
            p ++;
            焦耳/ =我;
         }
         C = 0;
         K = N;
         / *这背后while循环的数学？ * /
         而（K / I 0）
         {
            C + = K / I;
            K / =我;
         }
         NOZ =分钟（NOZ，C / P）;
      }
   }
   的printf（％d的％D尾随零的\ n！，N，NOZ）;

   返回0;
}
 

解决方案

请注意，这个问题就等于找到了的的最高权力基础的这把的 N！的

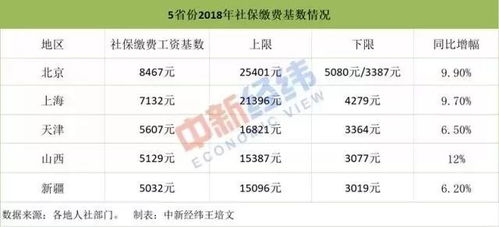
如果该基地是黄金（姑且称之为 P 的），我们可以使用的从数论定理来计算的 P 的是分裂的 N 的：

让我们来解压缩你code，这是否成为一个功能部分：

  INT maximum_power_of_p_in_fac（INT磷，INT N）{
    INT亩= 0;
    而（N / P大于0）{
        亩+ = N / P;
        N / = P;
    }
    返回亩;
}
 

现在发生什么，如果的基础的是一个主要的力量？比方说，我们拥有的基地= P ① 的。那么，如果的μ的是 P 的最高功率，其将的 N！和 R =地板（μ/ Q）的，我们有

（P ^ Q）^ R = P ^（QR）除以p ^μ分为N！

和

（P ^ Q）^（R + 1）= P ^（Q（R + 1））> = P ^（μ+ 1）做的没有的鸿沟N！

所以研究的是最大功率的点^ Q 的n个！让我们写一个函数，该函数还有：

  INT maximum_power_of_pq_in_fac（INT磷，INT Q，INT N）{
    返回maximum_power_of_p_in_fac（P，N）/ Q;
}
 

因此​​，如果的基础的是一般是多少？比方说，

基地= P 1 ① 1 P 2 ① 2 ... P M ① M

（这是的基地独特的因式分解的）。然后，我们就解决了所有的P 这个问题我 ①我 ，并取最小值那些：

  INT maximum_power_of_base_in_fac（INT基地，INT N）{
    INT RES =无穷大;
    每一个因子p ^ Q在基地的主要因子：
       RES =分钟（RES，maximum_power_of_pq_in_fac（P，Q，N））;
    返回水库;
}
 

如何因式分解的基础的？那么，我们可以只使用审判庭，就像你们的榜样code一样。我们首先检查是否2是一个主要因素。如果是，我们计算 maximum_power_of_pq_in_fac 和分裂的基础的按2，直到它不再整除然后，我​​们进行下一个候选的因素：

 无效比化（INT基地）{
    对于（INT P = 2; P＆LT; =基地; ++ P）{
        如果（碱％对== 0）{//如果基地整除用p，p是素因子
            INT Q = 0;
            而（基本％P == 0）{//计算q和摆脱所有的p因素
                q ++;
                底座/ = P;
            }
            //做些什么因子p ^ Q
        }
        //继续下一个候选除数
    }
}
 

通过仔细检查code，你会发现它包含上述所有因素，只有放在一起，在一个循环，这是一个有点混乱。

更新：如果你有兴趣，该算法你presented具有复杂的 O（基* log n）的的。您可以轻松地让它的 O（开方（基地）* log n）的的通过调整因式分解常规咯：

 无效比化（INT基地）{
    对于（INT P = 2; P * P＆LT; =基地; ++ P）{//只检查主要因素最多的sqrt（基地）
        // ...像以前一样
    }
    如果（基峰）{
        //恰好有一个主要因素＆GT;的sqrt（基峰）。
        //它肯定有多重1。

        //过程主要因素基地^ 1
    }
}
 

当然，你可以使用任何其他更复杂的质因子分解算法，如果你想加快速度，甚至更多。

The code below works perfectly but I would like someone to explain to me the mathematics behind it. Basically, how does it work?

#include <stdio.h> 
#include <stdlib.h>  /* atoi */

#define min(x, y) (((x) < (y)) ? (x) : (y))

int main(int argc, char* argv[])
{
   const int base = 16;
   int n,i,j,p,c,noz,k;

   n = 7;  /* 7! = decimal 5040 or 0x13B0  - 1 trailing zero */  
   noz = n;
   j = base;
   /* Why do we start from 2 */
   for (i=2; i <= base; i++)
   {
      if (j % i == 0)
      {   
         p = 0;  /* What is p? */
         while (j % i== 0)
         {
            p++;
            j /= i;
         }
         c = 0;
         k = n;
         /* What is the maths behind this while loop? */
         while (k/i > 0)
         {
            c += k/i;
            k /= i;
         }
         noz = min(noz, c/p);
      }
   }
   printf("%d! has %d trailing zeros\n", n, noz);

   return 0;
}

Note that the problem is equivalent to finding the highest power of base which divides n!.

If the base was prime (let's call it p), we could use a theorem from number theory to compute the highest power of p that divides n!:

Let's extract the part of your code that does this into a function:

int maximum_power_of_p_in_fac(int p, int n) {
    int mu = 0;
    while (n/p > 0) {
        mu += n/p;
        n /= p;
    }
    return mu;
}

Now what happens if base is a prime power? Let's say we have base = pq. Then if μ is the highest power of p which divides n! and r = floor(μ/q), we have

(p^q)^r = p^(qr) divides p^μ divides n!

and

(p^q)^(r+1) = p^(q(r+1)) >= p^(μ+1) does not divide n!

So r is the maximum power of p^q in n!. Let's write a function for that as well:

int maximum_power_of_pq_in_fac(int p, int q, int n) {
    return maximum_power_of_p_in_fac(p, n) / q;
}

So what if base is general number? Let's say

base = p1q1 p2q2 ... pmqm

(this is the unique prime factorization of base). Then we just solve the problem for all piqi and take the minimum of those:

int maximum_power_of_base_in_fac(int base, int n) {
    int res = infinity;
    for every factor p^q in the prime factorization in base:
       res = min(res, maximum_power_of_pq_in_fac(p,q,n));
    return res;
}

How to factorize base? Well we can just use trial division, like your example code does. We start by checking whether 2 is a prime factor. If it is, we compute maximum_power_of_pq_in_fac and divide base by 2 until it is no longer divisible by 2. Then we proceed with the next candidate factor:

void factorize(int base) {
    for (int p = 2; p <= base; ++p) {
        if (base % p == 0) { // if base is divisible by p, p is a prime factor
            int q = 0;
            while (base % p == 0) { // compute q and get rid of all the p factors
                q++;
                base /= p;
            }
            // do something with factor p^q
        }
        // proceed with next candidate divisor
    }
}

By examining the code carefully, you will find that it contains all the above elements, only put together in a single loop, which is a bit confusing.

UPDATE: In case you are interested, the algorithm you presented has complexity O(base * log n). You can easily make it O(sqrt(base) * log n) by adapting the prime factorization routine slightly:

void factorize(int base) {
    for (int p = 2; p*p <= base; ++p) { // only check prime factors up to sqrt(base)
        // ... same as before
    }
    if (base) {
        // there is exactly one prime factor > sqrt(base). 
        // It certainly has multiplicity 1.

        // process prime factor base^1
    }   
}

And of course you can use any other more sophisticated prime factorization algorithm if you want to speed things up even more.