我们给出的2 M 的阵列 - 1不同的，比较的元素，从1开始索引

我们可以查看阵列作为一个完全二叉树：

 节点放置在索引i。
左子放置在2I。
右子放在2I + 1。
 

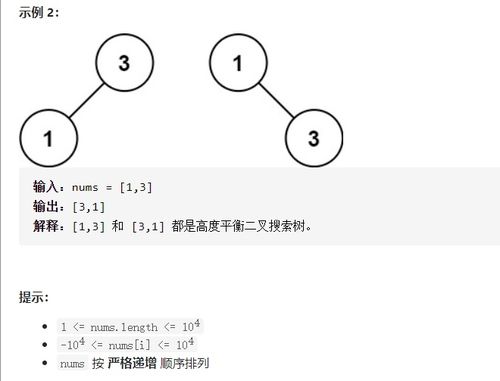
有关例如，该阵列

[7 6 4 5 2 3 1]

是树

  7
    / \
   6 4
  / \ / \
 5 2 3 1
 

现在作为一个二叉树查看时，这些元素满足堆属性，一个节点大于它的两个孩子：

A [1]＆GT; A [2I]和A [1]＆GT; A [2I + 1]

是否有相当快，原地算法洗牌的数组元素周围，使得所得的二叉树（如上所述）是一个二进制的搜索的树

回想一下，在一个二叉搜索树，一个节点大于其所有的左后裔，低于其所有的权利后代。

例如上述阵列的洗牌将是

[4 2 6 1 3 5 7]

其对应于二进制搜索树

  4
    / \
   2 6
  / \ / \
 1 3 5 7
 

解决方案

首先，我们注意到，我们可以 - 不失一般性 - 假设我们有元素1,2,3，... 2 ^我们的二叉树M-1 。所以，从现在开始，我们假定我们有这些数字。

然后，我尝试将一些功能转换一个排序的数组（即 1 2 3 4 5 ）到重$ P $阵列psenting的排序二叉树。

在一个排序二叉树（2 ^ M）-1 ​​元素，我们总是树的底是由所有的数字不均衡，如中为 M = 3 ：

  4
  2 6
 1 3 5 7
 

这意味着，相应的阵列中，我们有最后号都是不均匀的数字：

  4 2 6 1 3 5 7
      -------
         ^
         不平衡的数字！
 

因此​​，我们可以通过确保构建二进制树的最后的行，最后 2 ^（M-1）的相应阵列中的数字都是不均匀数字。所以，我们需要做的最后一排是构造一个函数，将所有元素的不均匀指数，最后一排的位置。

因此​​，让我们现在假设我们有一个程序是 - 给一个排序的数组作为输入 - 正确地确立了最后一排

然后我们可以调用子程序整个数组构造最后一排，而所有其他元素留下来排序。当我们应用在阵列上这个例程 1 2 3 4 5 6 7 ，我们有以下的情况：

  2 4 6 1 3 5 7
      -------
         ^
         正确！
 

在第一轮结束后，我们应用程序的其余子阵列（即 2 4 6 ），它构造了二叉树的倒数第二行，而我们离开其余元素不变，所以我们得到如下：

 现在是正确的！
   v
  ---
4 2 6 1 3 5 7
      -------
         ^
         正确的运行之前
 

因此​​，所有我们需要做的是建立一个功能，它安装的最后一行（即数组的后半部分）正确！

这可以在完成为O（n log n）的，其中 N 是阵列的输入大小。因此，我们只是遍历从一端到开头阵列和在这样一种方式，在最后一行（即后者的阵列的一半）是正确的交换不均匀的位置。这可以就地进行。之后，我们（使用如堆排序）第一阵列的一半进行排序。所以这个子程序的整个运行时间为O（n log n）的。

所以运行时的总规模 N 的数组是：

为O（n log n）的+ O（N / 2日志N / 2）+ O（N / 4日志N / 4）+ ... 这是同为O（n log n）的。请注意，我们必须使用一个就地排序算法，如堆排序，使这整个东西的作品完全原地。

我很抱歉，我不能进一步阐述，但我认为你可以得到的想法。

We are given an array of 2m - 1 distinct, comparable elements, indexed starting from 1.

We can view the array as a complete binary tree:

Node is placed at index i.
Left child is placed at 2i.
Right child is placed at 2i+1.

For instance, the array

[7 6 4 5 2 3 1]

is the tree

       7
    /    \
   6       4
  /  \    / \
 5    2   3  1 

Now when viewed as a binary tree, these elements satisfy the heap property, a node is greater than both its children:

A[i] > A[2i] and A[i] > A[2i+1]

Are there reasonably fast, in-place algorithm to shuffle the elements of the array around so that the resulting binary tree (as described above) is a binary search tree?

Recall that in a binary search tree, a node is greater than all its left descendants, and less than all its right descendants.

For instance the reshuffle of the above array would be

[4 2 6 1 3 5 7]

which corresponds to the binary search tree

       4
    /    \
   2       6
  /  \    / \
 1    3   5  7 

First we note that we can -- without loss of generality -- assume that we have the elements 1,2,3,... 2^m-1 in our binary tree. So, from now on, we assume that we have these numbers.

Then, my attempt would be some function to convert a sorted array (i.e. 1 2 3 4 5) into an array representing a sorted binary tree.

In a sorted binary tree with (2^m)-1 elements we have always that the "bottom" of the tree consists of all the uneven numbers, e.g. for m=3:

     4
  2     6
 1 3   5 7

This means, in the corresponding array, we have that the last numbers are all the uneven numbers:

4 2 6 1 3 5 7
      -------
         ^
         uneven numbers!

So we can construct the last "row" of the binary tree by ensuring that the last 2^(m-1) numbers in the corresponding array are all the uneven numbers. So all we need to do for the last row is to construct a function that moves all elements at positions with uneven indices to the last row.

So let us for now assume that we have a routine that -- given a sorted array as input -- establishes the last row correctly.

Then we can call the routine for the whole array to construct the last row while all other elements stay sorted. When we apply this routine on the array 1 2 3 4 5 6 7, we have the following situation:

2 4 6 1 3 5 7
      -------
         ^
         correct!

After the first round, we apply the routine for the remaining subarray (namely 2 4 6) which constructs the second last "row" of our binary tree, while we leave the remaining elements unchanged, so we get the following:

 now correct as well!
   v
  ---
4 2 6 1 3 5 7
      -------
         ^
         correct from run before

So all we have to do is to construct a function that installs the last row (i.e. the second half of the array) correctly!

This can be done in O(n log n) where n is the input size of the array. Therefore, we just traverse the array from end to the beginning and exchange the uneven positions in such a way that the last row (i.e. the latter half of the array) is correct. This can be done in-place. Afterwards, we sort the first half of the array (using e.g. heapsort). So the whole runtime of this subroutine is O(n log n).

So the runtime for an array of size n in total is:

O(n log n) + O(n/2 log n/2) + O(n/4 log n/4) + ... which is the same as O(n log n). Note that we have to use a in-place sorting algorithm such as Heapsort so that this whole stuff works completely in-place.

I'm sorry that I can't elaborate it further, but I think you can get the idea.